Page 66 - Ingeniantes Misantla 711

Revista Ingeniantes 2020 Año 7 No. 1 Vol. 1

donde Yi es un valor de los datos originales y λ es el
parámetro de la transformación. Los valores emplea-
dos en las transformaciones se muestran en la Tabla 3.

Tabla 3. Transformación de λ.

λ Transformación
2 = 2

0.5 = √
0 = ()
- 0.5 1 Figura 5. Distribución normal para 65 °C.
√1
-1 =
=

Se realiza la transformación de Box-Cox del valor λ -1 Figura 6. Distribución normal para 75 °C.
para las variables de temperatura de 60 °C y 65 °C y
λ – 0.5 para las variables de 75 °C. Según lo muestra la
Tabla 4.

Tabla 4. Resultados de la transformación de λ

λ Empleando 95% de confianza Modelo de regresión
Con los valores de cada una de las pruebas y los datos
Temperatura Estimar Lc Lc Valor de la pérdida de % de humedad afectada a cada una
Inferior superior redondo de las temperaturas sometidas al proceso de deshi-
dratación de 60 °C, 65 °C y 75 °C, en la Tabla 5 se
60 °C -0.86 -2.68 0.71 -1.00 establecen los modelos de regresión Y= a+bx, en con-
juto con su coeficiente de determinación que medirá la
65 °C -1.02 -2.79 0.52 -1.00 proporción de la variabilidad en los datos (Y) explicada
por el modelo de regresión mostrado en porcentaje,
75 °C -0.58 -2.08 0.95 -0.50 con valores de 0 al 100%, y determinación del menor
valor del error de estimación que indica la magnitud del
Para determinar si los datos siguen una distribución error de estimación de los modelos [8].
normal, se compara el valor p con el nivel de significan-
cia de 0.05 para las muestras de 60 °C, 65 °C y 75 °C Tabla 5. Modelos de regresión.
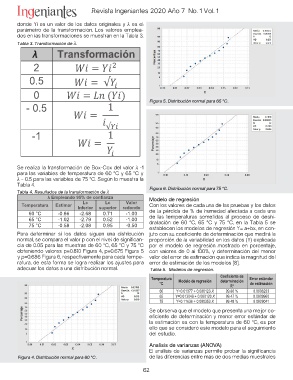
obteniendo valores p=0.810 Figura 4, p=0.675 Figura 5
y p=0.686 Figura 6, respectivamente para cada tempe-
ratura, de esta forma se logra realizar los ajustes para
adecuar los datos a una distribución normal.

Temperatura Modelo de regresión Coeficiente de Error estándar
°C Y=0.01377 + 0.000123 X determinación de estimación
Y=0.013049 + 0.000120 X
60 Y=0.11636 + 0.000353 X R² 0.0006233
65 99.80 % 0.0009960
75 0.0029041
99.47 %

99.48 %

Se obrserva que el modelo que presenta una mejor co-
eficiente de determinación y menor error estándar de
la estimación es con la temperatura de 60 °C, es por
ello que se consideró este modelo para el seguimiento
del estudio.

Figura 4. Distribución normal para 60 °C. Analisis de varianzas (ANOVA)
El análisis de varianzas permite probar la significancia
de las diferencias entre más de dos medias muestrales

62