Page 48 - ingeniantes Edicion interactiva 911

Revista Ingeniantes 2022 Año 9 No. 1 Vol. 1

Tabla 1. ConstanteTsablda e1: Cmonostadnetelsodesmcodoenloss ctoitnusttitiuvtoivoss una diferencia mínima se puede dar como validado el
modelo.
Modelo Polinomial 2do orden

D1=0.00000000 C10= 25.1267903 C01= -24.8977144 C02=-330.986926
D2=0.00000000 C20=-180.362444 C11=478.163660
D_I
Modelo MU_I Odgen 6to orden 0.00000000
I 19980.0632 ALPHA_I 0.00000000
1 -12463.3277 0.00000000
2 2490.09473 -1.53015512 0.00000000
3 1.25388094 0.00000000
-33413.1312 4.25655446 0.00000000
4 34466.6852
5 11060.5044 -6.65045249
-9.06608360
6
-11.4171028

Modelo C10= 0.556644823 Polinomial reducido 2do orden C02=0.00000000
D1=0.00000000 C20=3.43641517 C01= -0.00000000
D2=0.00000000 C11=0.00000000

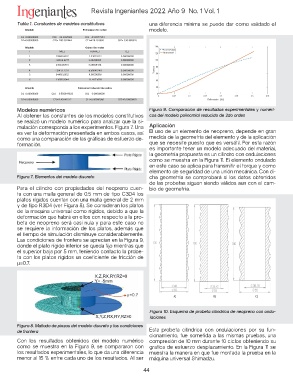
Modelos numéricos Figura 9. Comparación de resultados experimentales y numéri-
Al obtener las constantes de los modelos constitutivos cos del modelo polinomial reducido de 2do orden
se realizó un modelo numérico para analizar que la si-
mulación corresponda a los experimentos. Figura 7. Una Aplicación
es ver la deformación presentada en ambos casos, así El uso de un elemento de neopreno, depende en gran
como una comparación de las gráficas de esfuerzo de- medida de la geometría del elemento y de la aplicación
formación. que se necesite puesto que es versátil. Por esta razón
es importante tener un modelo adecuado del material,
Figura 7. Elementos del modelo discreto la geometría propuesta es un cilindro con ondulaciones
como se muestra en la Figura 11. El elemento ondulado
Para el cilindro con propiedades del neopreno cuen- en este caso se aplica para transmitir el torque y como
ta con una malla general de 0.5 mm de tipo C3D4 los elemento de seguridad de una unión mecánica. Con di-
platos rígidos cuentan con una malla general de 2 mm cha geometría se comprobará si los datos obtenidos
y de tipo R3D4 (ver Figura 8). Se consideran los platos de las probetas siguen siendo válidos aun con el cam-
de la maquina universal como rígidos, debido a que la bio de geometría.
deformación que habrá en ellos con respecto a la pro-
beta de neopreno será casi nula y para este caso no
se requiere la información de los platos, además que
el tiempo de simulación disminuye considerablemente.
Las condiciones de frontera se aprecian en la Figura 9,
donde el plato rígido inferior se queda fijo mientras que
el superior baja por 5 mm, teniendo contacto la probe-
ta con los platos rígidos un coeficiente de fricción de
µ=0.7.

Figura 8. Mallado de piezas del modelo discreto y las condiciones Figura 10. Esquema de probeta cilíndrica de neopreno con ondu-
de frontera laciones

Con los resultados obtenidos del modelo numérico Esta probeta cilíndrica con ondulaciones por su fun-
como se muestra en la Figura 9, se compararon con cionamiento, fue sometida a las mismas pruebas, una
los resultados experimentales, lo que da una diferencia compresión de 10 mm durante 10 ciclos obteniendo su
menor al 15 % entre cada uno de los resultados. Al ser grafica de esfuerzo desplazamiento. En la Figura 11 se
muestra la manera en que fue montada la prueba en la
máquina universal Shimadzu.

44