Page 20 - Ingeniantes 511 interactivo

Revista Ingeniantes 2018 Año 5 No. 1 Vol. 1

ferentes diseños, modelos, funciones y puntos de en Minitab [6] con los factores y respuestas antes
evaluación de cada uno de ellos. mencionados. En la Figura 1 se muestran los resulta-
• L a respuesta observada de la función es aquella dos obtenidos para el Modelo Esférico.

generada por Minitab [6] una vez hecha la opti-
mización para las variables de control.

• L a respuesta observada del modelo se obtiene
al sustituir los valores óptimos de las variables
de control en el modelo original utilizado.

• L a distancia para cada punto corresponde a
aquella entre los valores óptimos de las varia-
bles y cada uno de los diferentes puntos evalua-
dos en cada modelo.

• L a distancia al óptimo real representa la varia-
ción entre los valores óptimos de las variables
para cada punto de evaluación y el punto en el
cual se obtiene el mínimo global de cada mode-
lo.

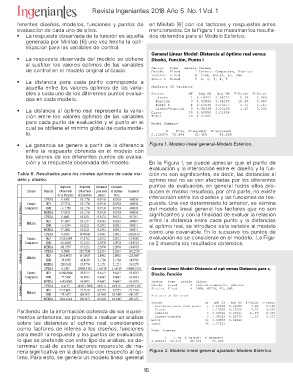
• La ganancia se genera a partir de la diferencia Figura 1. Modelo lineal general-Modelo Esférico.
entre la respuesta obtenida en el modelo con
los valores de los diferentes puntos de evalua- En la Figura 1, se puede apreciar que el punto de
ción y la respuesta observada del modelo. evaluación y la interacción entre el diseño y la fun-
ción no son significantes, es decir, las distancias al
Tabla 5. Resultados para los niveles óptimos de cada mo- optimo real no se ven afectadas por los diferentes
delo y diseño. puntos de evaluación, en general todos ellos pro-
ducen el mismo resultado, por otra parte, no existe
interacción entre los diseños y las funciones de res-
puesta. Una vez determinado lo anterior, se elimina
del modelo lineal general los factores que no son
significantes y con la finalidad de evaluar la relación
entre la distancia entre cada punto y la distancias
al optimo real, se introduce esta variable al modelo
como una covariable. En lo sucesivo los puntos de
evaluación no se consideran en el modelo. La Figu-
ra 2 muestra los resultados obtenidos.

Partiendo de la información obtenida de los experi- Figura 2. Modelo lineal general ajustado-Modelo Esférico.
mentos anteriores, se procede a realizar un análisis
sobre las distancias al optimo real, considerando
como factores de interés a los diseños, funciones
para medir la respuesta y los puntos de evaluación,
lo que se pretende con este tipo de análisis, es de-
terminar cuál de estos factores repercute de ma-
nera significativa en la distancia con respecto al óp-
timo. Para esto, se genera un modelo lineal general

16