Page 81 - Revista ingeniantes 2 No1 Vol 1 Interactiva
P. 81
Revista Ingeniantes Año 2 No. 1 Vol. 1
• Función de selección.- elegir la moneda de ma- RESULTADOS Y CONCLUSIONES
yor valor posible tal que satisfaga las restriccio- Al realizar la ejecución de estos algoritmos por
nes de factibilidad. utilizando como herramienta Matlab ®. Con un sis-
tema monetario ficticio {60, 40, 10, 6, 4, 1} se obtu-
El algoritmo resultante de este proceso es de vieron los siguientes resultados:
orden n con respecto al número de monedas. Ambos algoritmos se comportan de una forma
Sin embargo este algoritmo depende del sistema aceptable, sin embargo el algoritmo voraz con
monetario que se ocupa en cada país, pudiendo este sistema monetario produjo resultados no óp-
no dar el mejor resultado bajo ciertas caracterís- timos, mientras que el algoritmo dinámico, siem-
ticas de dicho sistema. Por ejemplo {6, 4, 1} y {11, pre devolvió mejores soluciones.
5, 1}. En estos sistemas monetarios este algoritmo El algoritmo dinámico es más barato en tiempo de
produciría resultados no óptimos. ejecución que el algoritmo voraz para el cálculo
Solución Dinámica de múltiples valores a devolver.
El algoritmo dinámico se basa en llenar una tabla Este algoritmo en su implementación de forma
C conformada por tantas filas como denomina- general utiliza dos tablas una para el cálculo y una
ciones de monedas hay, y las columnas serán las copia de esta para la búsqueda de las soluciones,
cantidades entre 1 y el valor a devolver, de esta lo que implica un gran requerimiento de memoria
manera se calcularan todas las formas posibles RAM, sin embargo con una pequeña modificación
de devolver entre 1 y la cantidad requerida ha- y calculando por métodos estadísticos cuál es el
ciendo uso de las diferentes denominaciones que mayor cambio que puede devolver la máquina ex-
se tienen. pendedora, es posible utilizar la misma tabla para
Por lo tanto devolver una cantidad estará relacio- ambas tareas. Devolviendo el tipo de las monedas
nado con las denominaciones utilizadas y con la a devolver y la cantidad de cada una de ellas.
soluciones de devolver cantidades inferiores. La función de recorrido la cual tiene un orden de
Donde el numero almacenado en C[i][j] será el ejecución menor a n siendo n la cantidad a devol-
número mínimo de monedas necesarias para de- ver. Este hecho compensa la cantidad de memoria
volver j unidades, haciendo uso de las primeras que ocupa la tabla en el sistema.
i denominaciones y T[i], es la i-ésima denomina- Para este trabajo se realizaron las pruebas para
ción, y se calcula de la forma que se observa en la devolución con monedas de las siguientes can-
la figura 1. tidades en el rango de 1 hasta la cantidad 100 con
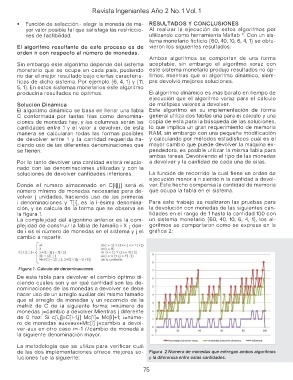
La complejidad del algoritmo anterior es la com- un sistema monetario {60, 40, 10, 6, 4, 1}, los al-
plejidad de construir la tabla de tamaño i X j don- goritmos se comportaron como se expresa en la
de i es el número de monedas en el sistema y j el gráfica 2:
cambio a repartir.
Figura 1. Cálculo de denominaciones Figura 2Número de monedas que entregan ambos algoritmos
y la diferencia entre estas cantidades.
De esta tabla para devolver el cambio óptimo di-
ciendo cuales son y en qué cantidad son las de-
nominaciones de las monedas a devolver se debe
hacer uso de un arreglo auxiliar del mismo tamaño
que el arreglo de monedas y un recorrido de la
matriz de C de la siguiente forma: i=número de
monedas j=cambio a devolver Mientras j diferente
de 0 haz: Si c[i,j]≥C[i-1,j] Mc[i]= Mc[i]+1; i=núme-
ro de monedas aux=aux+Mc[i] j=cambio a devol-
ver-aux en otro caso i=i-1 //cambio de moneda a
la siguiente denominación mayor.
La metodología que se utiliza para verificar cuál
de las dos implementaciones ofrece mejores so- Figura 2 Número de monedas que entregan ambos algoritmos
luciones fue la siguiente: y la diferencia entre estas cantidades.
75